Resolvido 142 ENEM 2023 Matemática

Questão 142

Sejam a, b e c as medidas dos lados de um triângulo retângulo, tendo a como medida da hipotenusa. Esses valores a, b e c são, respectivamente, os diâmetros dos círculos C1, C2 e C3, como apresentados na figura.

Um professor de matemática era conhecedor dessa construção e, confraternizando com dois amigos em uma pizzaria onde são vendidas pizzas somente em formato de círculo, lançou um desafio: mesmo sem usar um instrumento de medição, poderia afirmar com certeza se a área do círculo correspondente à pizza que ele pedisse era maior, igual ou menor do que a soma das áreas das pizzas dos dois amigos. Assim, foram pedidas três pizzas. O professor as dividiu ao meio e formou um triângulo com os diâmetros das pizzas, conforme indicado na figura.

A partir da medida do ângulo a, o professor afirmou que a área de sua pizza é maior do que a soma das áreas das outras duas pizzas.

A área da pizza do professor de matemática é maior do que a soma das áreas das outras duas pizzas, pois

A 0° < a < 90°

B a = 90°

C 90° < a < 180°

D a = 180°

E 180° < a < 360°

Resolução:

Vamos começar analisando a situação que alfa = 90° e teremos um triângulo retângulo, podendo escrever o Teoremas de Pitágoras pra ele. Vou chamar de D o diâmetro da pizza e R o raio da Pizza. Já conhecemos há muito tempo a relação entre diâmetro e raio, que é D = 2.R (o diâmetro vale o dobro do raio)

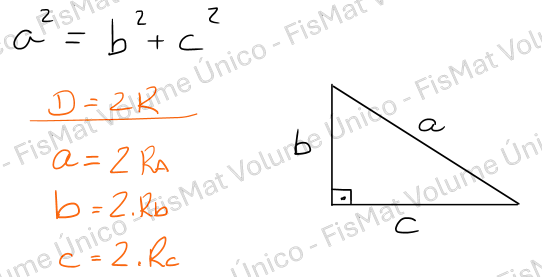
No triângulo acima, a, b e c são os diâmetros das pizzas. Substituindo então em Pitágoras, podemos desenvolver a equação. Passos:

• resolver as potências

• dividir a equação por 4

• multiplicar a equação por Pi para obter a fórmula da área da pizza, que é um círculo.

Assim, podemos provar que há uma relação entre as áreas dor círculos do desenho do enunciado.

Veja que o resultado acima nos indica que, para alfa = 90°, a área da pizza maior (professor) é igual a soma das áreas das pizzas menores (amigos). Como o professor afirmou que a área da sua pizza é maior que a soma das áreas das pizzas dos amigos, então vamos ver abaixo o que acontece com os diâmetros ao alterar o valor do ângulo alfa:

Acima, vamos manter os lados pretos do mesmo tamanho e alterar apenas o ângulo alfa colorido. Veja que, começando do ângulo alfa azul, temos o lado azul que é o diâmetro da pizza do professor. Depois, aumentando alfa para o ângulo laranja, o lado laranja aumenta, com isso o diâmetro da pizza do professor aumenta e, portanto, a área da pizza do professor aumenta. Por fim, aumentamos mais ainda o ângulo alfa para o ângulo verde, o lado verde representa o diâmetro da pizza do professor, que aumentou mais ainda, aumentando também a área da pizza. Assim, podemos concluir que o valor do ângulo alfa tem uma relação direta com o lado oposto a esse ângulo e, com a área da pizza do professor. Quanto mais Alfa aumenta, maior fica a área da pizza do professor.

Jà que para alfa = 90° a área da pizza do professor é igual à soma das áreas das pizzas dos amigos, então, para que a área da pizza dele seja maior do que a soa das áreas dos amigos, o ângulo alfa deve ser maior que 90° e estar entre 90° e 180°.

Resposta:

C